이번 글에서는 Balanced Tree의 종류 중 하나인 B 트리를 알아보고 다음 글에서는 B 트리를 개선한 B+ 트리를 알아보겠습니다.
B 트리 (B-Tree)
B 트리의 목적은 트리의 높이를 줄이는 것입니다. 트리 자료구조에서 트리의 높이가 높아질수록 탐색하는 시간이 길어집니다.
B 트리는 하나의 노드에 여러 데이터가 배치되는 트리구조입니다. 한 노드에 최대 M개의 자료가 배치된다면 M차 B 트리 라고 부릅니다.
노드의 데이터 개수가 N이라면 노드의 자식 수는 N + 1이어야 합니다. 또한 각 노드의 자료는 정렬된 상태여야합니다. 또한 루트 노드를 제외한 모든 노드는 최소 M / 2개의 데이터를 가지고 있어야 합니다. 또한 입력 데이터는 중복될 수 없습니다.
마지막으로 단말 노드(leaf node)가 모두 같은 레벨에 있어야합니다.
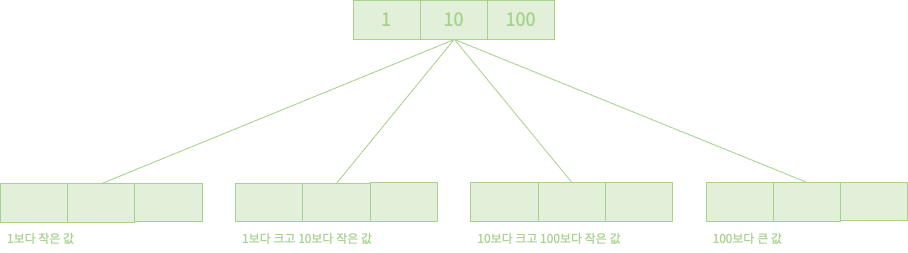
위는 3차 B 트리입니다. 위 예제에서 루트 노드의 데이터 개수는 3개입니다. 그렇기 때문에 자식 노드의 3 + 1 즉 4개가 됩니다. 이렇게 본다면 왜 N + 1개가 있어야 하는지 쉽게 이해할 수 있겠죠?
B 트리 탐색
B 트리의 탐색은 아래와 같이 이루어집니다.
노드 내부의 데이터는 순회하며 탐색합니다.
루트노드부터 시작하며 재귀적으로 이루어집니다.
1. 현재노드의 첫번째 키보다 탐색 데이터가 작다면 왼쪽 서브트리에서 데이터를 찾습니다.
2. 현재노드의 데이터를 순회하며 탐색 데이터가 현재 데이터보다 작다면 왼쪽 서브트리를 탐색합니다.
3. 현재노드의 마지막 키보다 클 경우 오른쪽 서브트리를 탐색합니다.
4. 현재 노드가 단말 노드(leaf node)일 경우 NULL을 반환합니다.

위와 같은 B 트리에서 4라는 데이터를 탐색해보겠습니다.
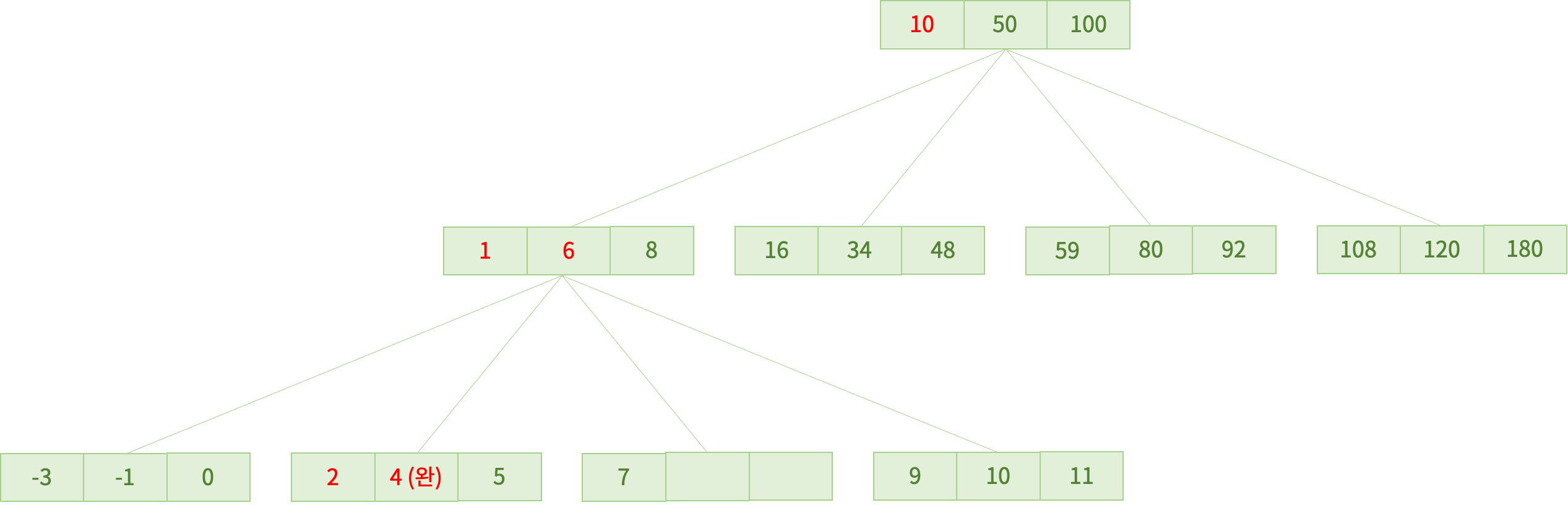
1. 먼저 루트 노드의 10보다 작기 때문에 왼쪽 서브트리로 갑니다.
2. 왼쪽 서브트리에서 4는 1보다 크기 때문에 다음 데이터로 이동합니다.
3. 4는 6보다 작기 때문에 왼쪽 서브트리로 내려갑니다.
4. 2보다 크기 때문에 다음 데이터로 넘어갑니다.
5. 탐색 완료
B 트리 삽입
트리의 M(차수)이 홀수인가 짝수인가에 따라 방식이 달라집니다. 이번 예시는 3차 B 트리로 설명하겠습니다.
1. 루트 노드를 할당하고 데이터를 삽입한다.
2. 삽입할 적절한 노드를 검색한다.
3. 노드가 가득 찬 경우
- 중간값을 부모 노드로 트리를 분할하여 구성합니다.
- 분리된 서브트리가 B 트리의 조건에 맞지 않다면 부모 노드로 올라가며 병합합니다.B 트리 삭제
삭제는 몇가지 경우로 나누어 설명하겠습니다.
단말 노드
단말 노드이며 데이터를 삭제해도 B 트리를 유지한다면 데이터를 검색 후 삭제합니다.
하지만 데이터를 삭제했을때 B 트리를 유지하지 않는다면 아래와 같은 방법을 통해 삭제합니다.
1. 삭제한 노드의 부모 노드로 올라가며 데이터를 가져옵니다.
2. 데이터보다 하나 많은 자식 노드의 개수를 유지하기 위해 부모노드와 형제 노드를 병합합니다.
3. 계속 부모노드로 올라가며 B 트리의 조건이 맞을때 까지 작업을 반복합니다.단말 노드가 아닐 경우
단말 노드가 아닐 경우 아래와 같은 방식으로 삭제합니다.
1. 노드에서 데이터를 삭제하고 왼쪽 서브트리에서 최대값을 노드로 가지고 옵니다.
2. 같은 방식으로 부모노드에서 자식노드로 값을 가져오고 형제노드와 병합하며 B 트리의 조건이 맞을때 까지 반복합니다.왜 DB는 B트리를 사용할까?
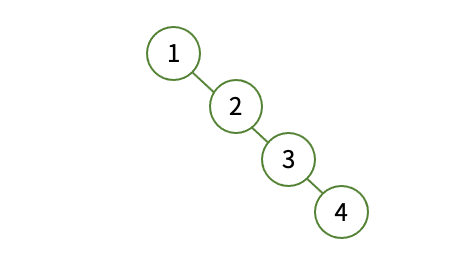
위와 같은 트리의 Worse case에서 탐색 시간은 O(N)의 시간복잡도를 가집니다. 하지만 Balanced Tree는 삽입, 삭제 시 노드의 높이를 일정하게 맞춰주기 때문에 최악의 경우도 O(logN)의 시간 복잡도를 가집니다.
이제부턴 제가 직접 받았던 면접 질문입니다.
"그렇다면 왜 O(1)의 해시 자료구조를 사용하지 않고 B 트리를 사용했을까요?"
해시를 사용하지 못하는 이유는 해시는 하나의 데이터를 탐색하는 시간이 O(1)이기 때문입니다. DB에서는 =이 아닌 >, <와 같은 부등호도 사용할 수 있습니다.
해시는 데이터가 정렬되어 있지 않기에 매우 비효율적입니다.
그에 비해 트리는 정렬되어있기 때문에 효율적으로 데이터를 탐색할 수 있습니다.
"그렇다면 다른 트리를 사용하면 되지 않나요?"
다른 O(logN)의 트리를 사용하면 되지 않을까라는 생각이 들 수 있습니다. 하지만 B 트리는 다른 트리와 달리 하나의 노드에 데이터가 순차적으로 삽입되어 있습니다. 이는 메모리에 연속적으로 저장되어있다는 것을 의미합니다. 그렇기 때문에 노드와 노드사이의 이동은 참조로 이동하지만 노드 내부의 데이터는 순차적으로 이루어집니다.
그렇다면 같은 O(logN)의 시간복잡도를 가져도 물리적으론 B 트리가 더 빠르게 탐색할 수 있다는 것입니다.
아래와 같이 정리할 수 있을 것 같습니다.
1. 항상 정렬된 상태이기에 부등호 연산에 유리하다
2. 참조 포인터가 적어 빠르게 메모리 접근이 가능하다
3. 데이터 탐색뿐 아니라 삽입, 삭제에도 O(logN)의 시간 복잡도를 가진다
참고 문서
더 자세한 내용은 아래 글에서 정리되어 있습니다.
B-Tree 개념 정리
'개발 > 알고리즘, 자료구조' 카테고리의 다른 글
| Array List와 Linked List (0) | 2021.04.15 |
|---|---|
| [알고리즘] 조합, 순열 알고리즘 (파이썬) (0) | 2021.01.30 |
| [자료구조] 힙 (Heap) (0) | 2021.01.25 |
| [자료구조] 트리 (Tree) (0) | 2021.01.22 |
| [자료구조] 해시 테이블 (Hash Table) (0) | 2020.12.07 |